theoriz3r
theoriz3r is a tool to do exploratory automated theorem proving.
1. Motivation
Question machines
See the context described here: https://tsvibt.blogspot.com/2022/06/multisheets-multi-dimensional.html#context.
In short, the idea is to automate some aspects of propagating stated beliefs. The automated belief-propagator can point out to the user contradictions in their explicit beliefs, and can point the user to questions that they haven't yet explicitly answered, skipping over all the questions that are answered as routine consequences of the beliefs they've already stated. The payoff is that the user gets to be feed a line of questions that are automatically selected to be at least a little more interesting than a random question.
This post describes an instance of that pattern.
Example: topological spaces and properties
So, as a motivating example, consider point-set topology. We have spaces ($\mathbb{R}$, $S^2$, a singleton, etc.), we have properties of spaces (Hausdorff, connected, metrizable, etc.), we have functions between spaces, and so on.
What's interesting here is that even with a very simple ontology, there are already many questions, many of them interesting (and many of them not interesting). We can restrict to just two sorts of things: spaces and properties of spaces. We immediately get a huge list of questions. For each space and each property, does that property hold of that space? For each property, is there a space with that property, and one without that property? For each set of properties (including negations), is there a space that satisfies all those properties simultaneously?
To see that there are many interesting questions of this form, one only needs to flip through Steen and Seebach's book, Counterexamples in topology.
To see that there are many uninteresting questions, consider these properties of spaces: arc connected (connected by injective paths), path connected (connected by paths), and connected (can't be separated). Once one has recognized that arc connected implies path connected, and path connected implies connected, what about the question: is there a space that's arc connected but not connected? The answer is trivially "no", by propositional logic. This should be recognizable in an automated way.
As another example, suppose we know that there is a space that is not first countable, and we know that there is a space that's not connected. Now we ask: is there a space that's both not first countable and also not connected? A simple idea suffices: the sum of the two spaces will fail to be first countable and fail to be connected. But now we have a general recipe. Many properties are preserved in some way through operations like summation. A sum is first countable if and only if both summands are first countable, and likewise metrizable, compact, and so on. So we should be able to just state these preservation properties, and state the existence of basic examples (e.g. of a non-metrizable space) and have a large swath of questions removed from our attention automatically: there's no interesting question as to whether there's a space that is both non-metrizable and not first countable.
2. Using Z3
Z3 is an SMT solver. I don't know how it works in detail, so everything I say about it should be considered pretty uncertain and possibly confused.
Anyway, Z3 can be used as a finite model checker: you define some objects and some functions (e.g. boolean-valued, i.e. properties), input a list of propositions (boolean-valued terms), and the solver says "satisfiable" and gives a model, says "unsatisfiable" and gives a minimal set of unsatisfiable input propositions, or says "timeout" if it took too long.
theoriz3r
theoriz3r is:
- a wrapper around z3, to make it convenient to deal with certain stereotyped theories; and
- some scripting to iterate over questions and cache answers to improve performance.
So to use theoriz3r, you write a file such as top.py that:
- declares some types (usually just one, in this case
Top), objects, properties, and functions (not too many); and
- makes some assertions about which properties apply to which objects, and which properties imply other properties.
Then you call theoriz3r, which:
- checks that the input propositions are consistent; and
- produces a list of questions that haven't been answered by the input propositions.
Examples
§ The basic apparatus
Here's a toy example of theoriz3r working:
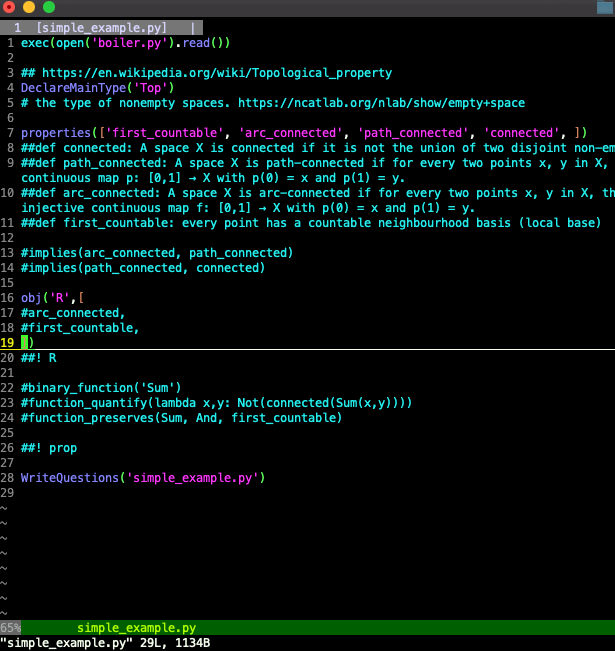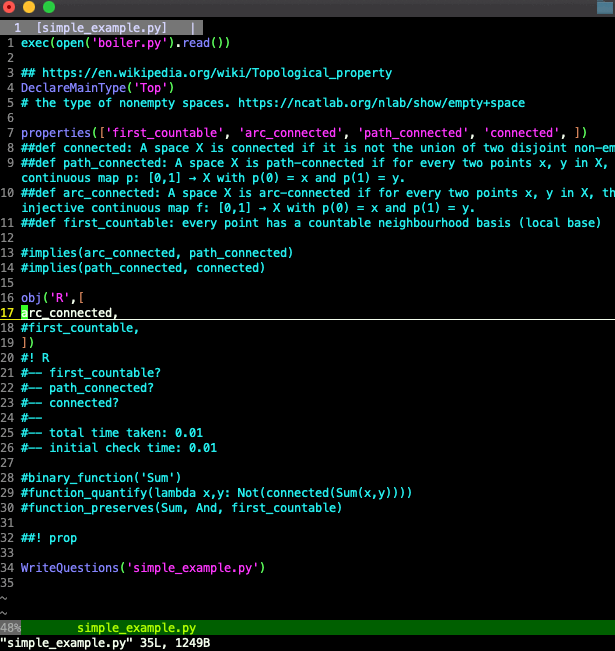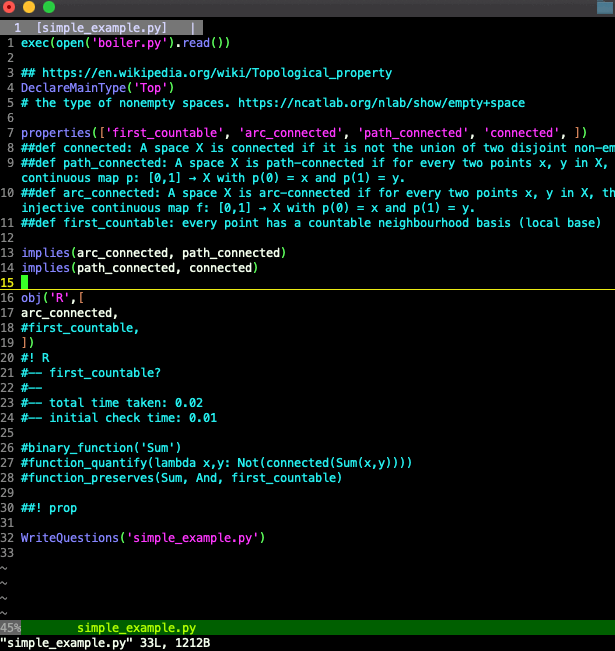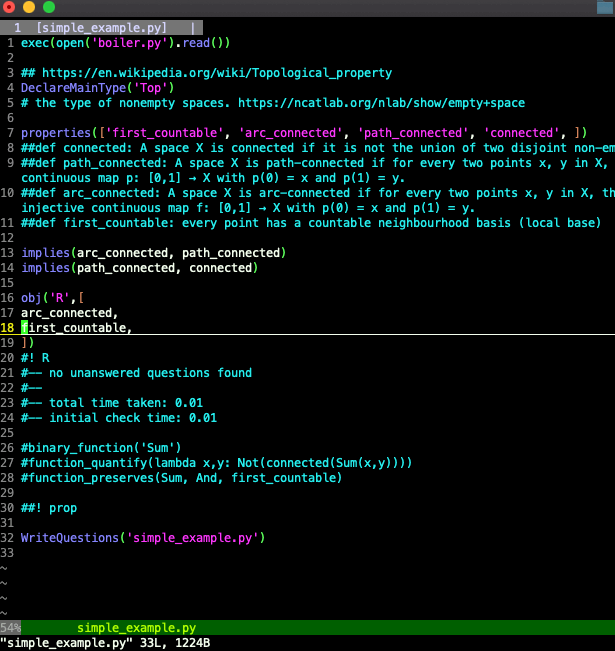
To step through what's happening:
The basic outer loop for using theoriz3r is:
- Edit the file by adding properties, objects, functions, theorems, definitions, and commands.
- Run the file as a python script. The python script edits the file, displaying results.
In this gif, each time I make an edit, I then run the file simple_example.py as a python script. Each time I do that, the first thing that happens is that theoriz3r is executed. That's the first line, though it would now read
exec(open('theoriz3r.py').read())
Executing theoriz3r.py defines methods used in the rest of simple_example.py.
Next, Top is defined as the main type of object for this file. Then some properties are added; intuitively this says "these are some properties that can hold or not hold of a given Top object". By adding these properties, we ask theoriz3r to look for questions about the main type (Top) involving these properties.
Then the object R is asserted to exist, it's assumed to be of the main type, and it's declared to satisfy some properties (it's arc connected and first countable).
Then some theorems are assert. E.g. one says "any object of type Top, if it satisfies arc_connected, then it also satisfies path_connected. Under the hood, in Z3's language, that theorem looks like:
ForAll(X, Implies(arc_connected(X), path_connected(X)))
Finally, WriteQuestions is called on this file. Now what happens is that theoriz3r looks for the first line in the file that starts with #!. That indicates a commond line. Then theoriz3r writes the results of the command after the command line.
If the rest of the command line is the string "prop", then theoriz3r lists out sets of properties which have not yet been determined to be satisfiable or unsatisfiable by the objects declared to exist (and the theorems declared to hold).
If the rest of the command line is not the string "prop", then theoriz3r finds the object most recently defined above the command line. Then theoriz3r figures out, from the properties asserted of that object and from the theorems assert, which properties must hold or must not hold of the object. Any other properties, ones that were declared but that weren't already decided to hold or not hold of the object, will be listed as results.
§ Object questions
Looking at the same example again:

First, with stuff commented out, there are no properties asserted of R. So all the properties declared to exist are open questions about R. Is R first countable, or no? And so on.
Then with arc_connected uncommented, R is asserted to be arc connected. Executing the file again, we get a reduced list of open questions about R: "arc_connected?" doesn't appear any more because R is now proved (by assertion) to be arc connected.
Next, with the line
implies(arc_connected, path_connected)
uncommented, path connectedness also disappears from the list of open questions. theoriz3r checks to see if it's satisfiable to have that R is not path connected. It finds that no, that is not satisfiable, because by the theorem asserted and because R is asserted to be arc connected, R is also path connected.
With the line
implies(path_connected, connected)
uncommented, we see a glimpse of the work that theoriz3r is doing for us. With that general theorem, which will apply to any other topological spaces we declare to exist, we can just say that a space is arc connected, and that will imply that the space is both path connected and connected. The point isn't that the resulting conclusion isn't obvious. The point is just that theoriz3r automatically goes through lots of these obvious conclusions, and only asks us about what's left, which tend to be more interesting questions.
§ Property questions
Here's the next example:
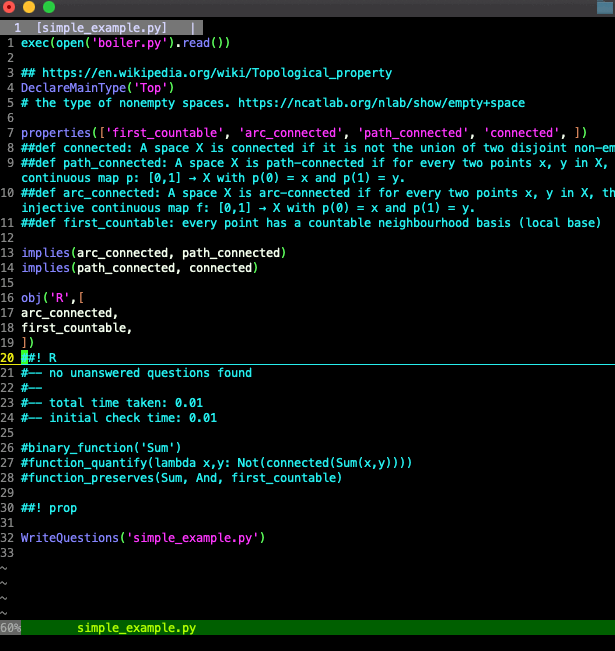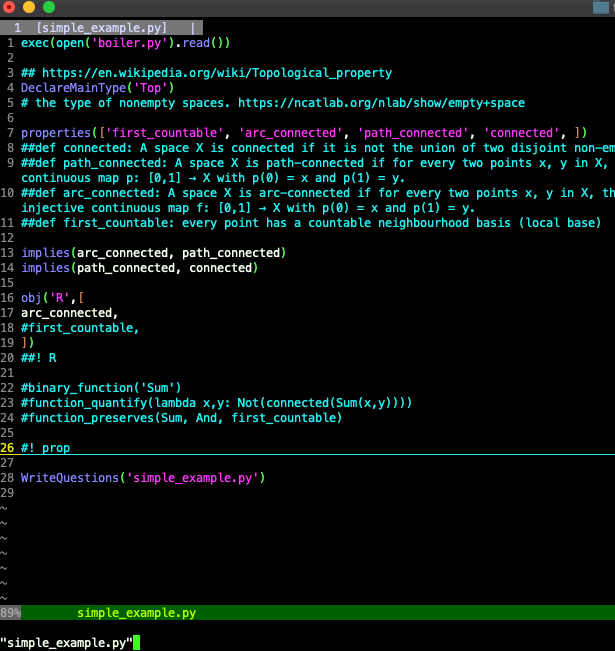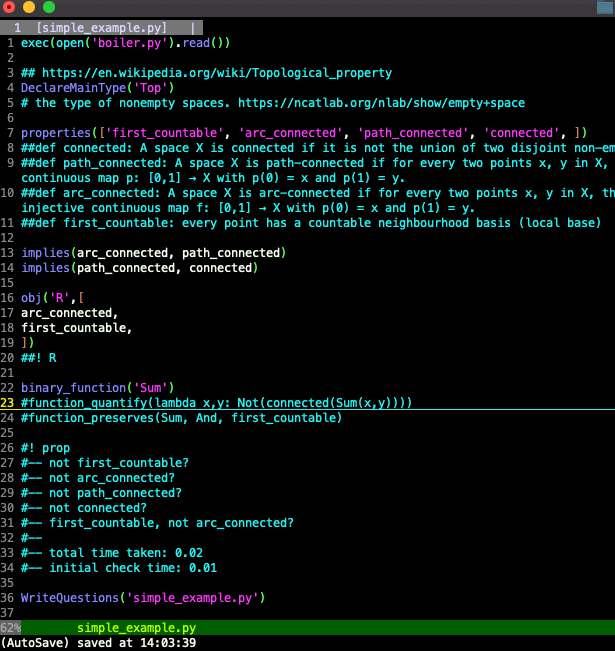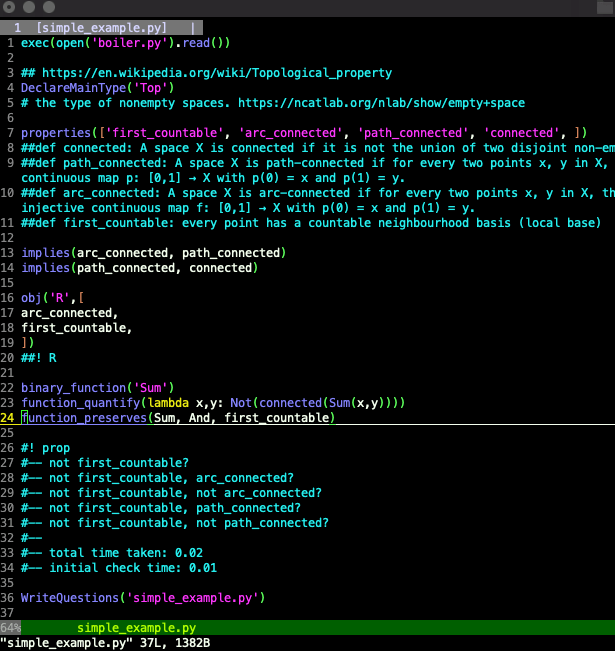
In this example the command line reads
#! prop
so theoriz3r lists out sets of properties that have not yet been determined to be, in conjunction, satisfiable or unsatisfiable by a single topological space.
At the start, it's already been determined that it's possible for a space to be arc connected, it's possible for a space to be path connected, and it's possible for a space to be connected. That follows from R being arc connected and the theorems.
What hasn't been determined is whether it's possible for a space to be first countable, or whether it's possible for a space to not be arc connected, and so on. So those properties show up as questions.
The line
binary_function('Sum')
asserts that there exists a function Sum; it's assumed to be of type Top×Top⟶Top. This asserts the existence of objects Sum(R,R), Sum(R,Sum(R,R)), and so on. When constructing models, Z3 will try to "pun" objects to keep the model as small as possible, e.g. it will at first try to set Sum(R,R) = R so that there's only one object. When that doesn't work, Z3 adds more objects. Unfortunately, that means model checking can easily explode to be expensive or impossible (first order logic is not in general decidable). So functions should be used sparingly.
The next line
function_quantify(lambda x,y: Not(connected(Sum(x,y))))
adds a proposition which says that the sum of any two spaces is not connected. (We're assuming spaces are nonempty.) Without any more work, this assertion closes most of the remaining single-property questions. Since R exists, Sum(R,R) exists. By the assertion, Sum(R,R) is not connected. By the other two asserted theorems, if Sum(R,R) is not connected, then it is also not path connected and not arc connected. So it is possible for a space to be not connected, and so on. Note that, as implemented, theoriz3r doesn't actually assert the general property of Sum, but instead just asserts the preservation property where x and y are base objects (in the present case, just R); this saves potentially a lot / infinitely much on performance, but gives less powerful inference.
Leaving aside the single-property question of whether there exists a space that's not first countable, we look at the first two-property question:
#—— first_countable, not arc_connected?
We can answer this and lots of other questions in one swell foop by asserting:
function_preserves(Sum, And, first_countable)
This says that the function Sum preserves first countability if both arguments (And) have the property. Now the two-property question "Can there be a space that is first countable but not arc connected?" is automatically answered: since R is first countable, so is Sum(R,R), and we know that Sum(R,R) is not connected and therefore not arc connected. So it is impossible for there to not exist a space that is first countable and not arc connected.
§ Contradictions
Here's the final example:
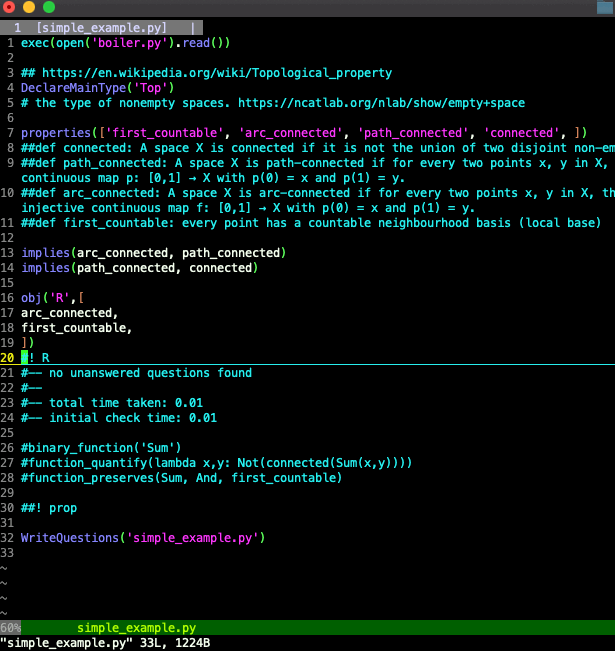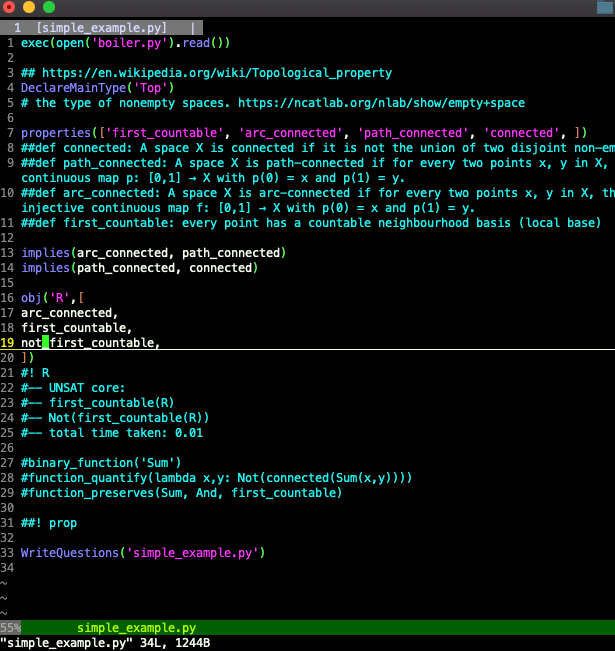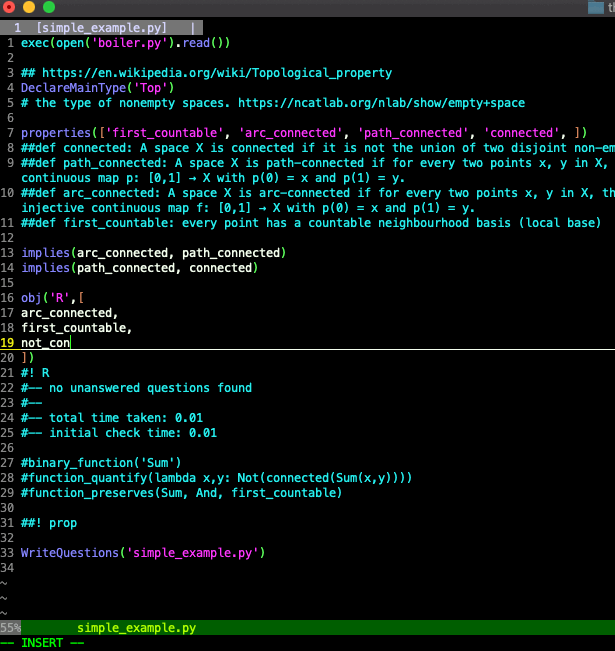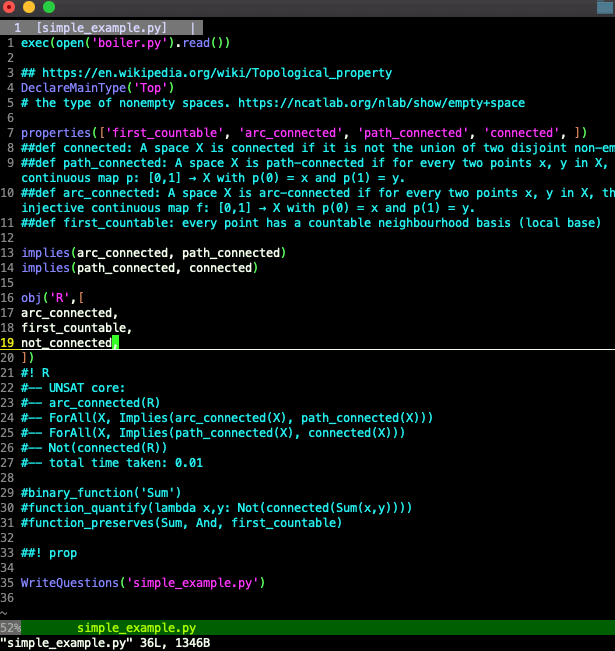
What happens if we assert that R is both first countable and not first countable? theoriz3r tells us that there's a problem with what we've said, and tells us an unsatisfiability core——a minimal set of statements we've asserted that are contradictory:
#—— UNSAT core: #—— first_countable(R) #—— Not(first_countable(R))
Unsatisfiability cores are helpful when the contradiction isn't so blatant. E.g. here we're told the theorems that make it a contradiction to say that R is arc connected but not connected:
#—— UNSAT core: #—— arc_connected(R) #—— ForAll(X, Implies(arc_connected(X), path_connected(X))) #—— ForAll(X, Implies(path_connected(X), connected(X))) #—— Not(connected(R))
As a more real example that I actually ran into when using theoriz3r to talk about real functions:
#—— UNSAT core: #—— ForAll(X, Implies(And(even(X), odd(X)), constant(X))) #—— even(indicator_0) #—— odd(indicator_0) #—— Not(constant(indicator_0))
I'd asserted that if a function is both even (symmetric about 0) and odd (anti-symmetric about 0), then it is a constant function. I'd also asserted that the indicator function of 0, i.e. 0-valued everywhere except 1-valued at 0, is even and odd and not constant. theoriz3r told me my mistake.
Using theoriz3r
The code for theoriz3r is here: https://github.com/tsvibt/theoriz3r/
If you have trouble getting it to work but want to try it, feel free to contact me.
If you have some familiarity with topology, I recommend starting with top.py. You use it by looking at the questions that theoriz3r produces.
If they are questions about an object (the command line will look like #! name_of_object) then try to add properties to the object (that actually hold of the object!) that resolve the question by determining that the object has the property or doesn't have the property. Or, resolve the question by adding theorems——do this if the answer to the question "ought to be obvious" from what you've already declared about the object.
If they are questions about properties (the command line will look like #! prop) then try to add objects, properties of objects, or theorems to resolve the question: can this property / this list of properties be simultaneously satisfied by a single object (e.g. a single topological space)? If you think the answer is yes, add an object, or assert that an object you've already added has these properties (or maybe add a function that produces objects and add theorems saying what properties will hold of the result of that function). If you think the answer is no, assert a theorem to that effect. Try to make it a strong, general theorem.
3. Aspirations for exploratory provers
theoriz3r is just a proof of concept. The concept that's being hopefully proved, or at least gestured at, is a kind of "exploratory automated theorem prover". Formal theorem proving uses the power of computers to make it manageable to formally prove lots of interesting statements from a small set of basic trusted axioms. Exploratory automated theorem proving is aimed at making it faster and more fun to play around with interesting statements. Formal theorem proving distrusts the user, raising an issue when a statement hasn't yet been proved; exploratory proving mostly takes the user's statements on faith, only raising an issue when some asserted statements have been refuted by being contradictory to other asserted statements.
theoriz3r works with Z3, which is most straightforward to use for theories with small finite models. This isn't the natural language of math. There's nothing in principle stopping one from making an exploratory theorem prover that uses a fully expressive logic. Instead of Z3's model checking, such an exploratory prover would have to do some bounded, heuristically-directed proof search. There'd be no hope of a complete procedure, but there never really was such a hope anyway.
I think I read somewhere that people who use Lean will sometimes put assert everywhere at first in some context, just laying things out and only filling in some later parts of proofs, before going back to fill in the rest. That sounds kinda like a form of exploratory proving. I haven't tried that so I don't know what it's like. I wonder if that style could be developed and tooled to be an active exploratory mode.
In general the idea is:
- Maintain a list of propositions asserted by the user.
- Look for contradictions in those assertions (by whatever means——model checking, brute-force proof search, heuristics, ...), and tell the user if a contradiction is found.
- Maintain a list of question machines——programs that generate propositions.
- When the user asks for open questions, use the question machines to generate propositions and then check (again, by whatever means) whether the propositions can already be shown true or false by the existing list of user-assertions. Give the user questions that aren't already answered that way.