TL;DR: To keep track of your thoughts about a question that has multiple parameters, you can use multi-dimensional spreadsheets. If you use vim, vim-multisheets is a basic implementation of multi-dimensional spreadsheets; code here. Tracking beliefs and then automatically unfolding some of their consequences can point towards questions you haven't answered and point to contradictions in your beliefs.

Teaser

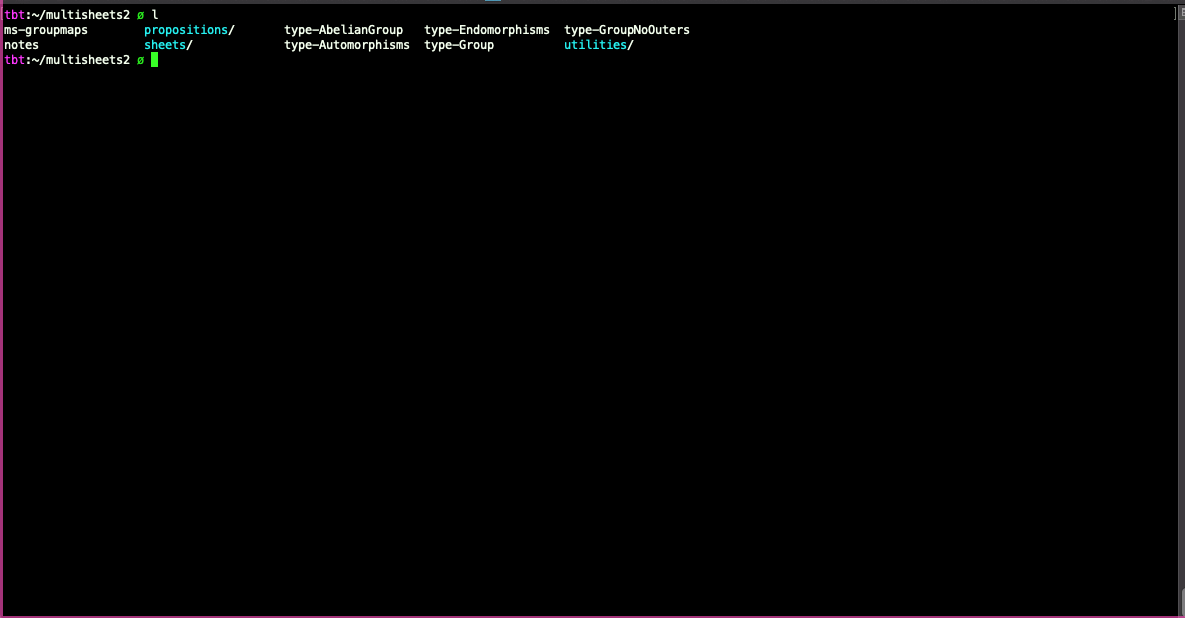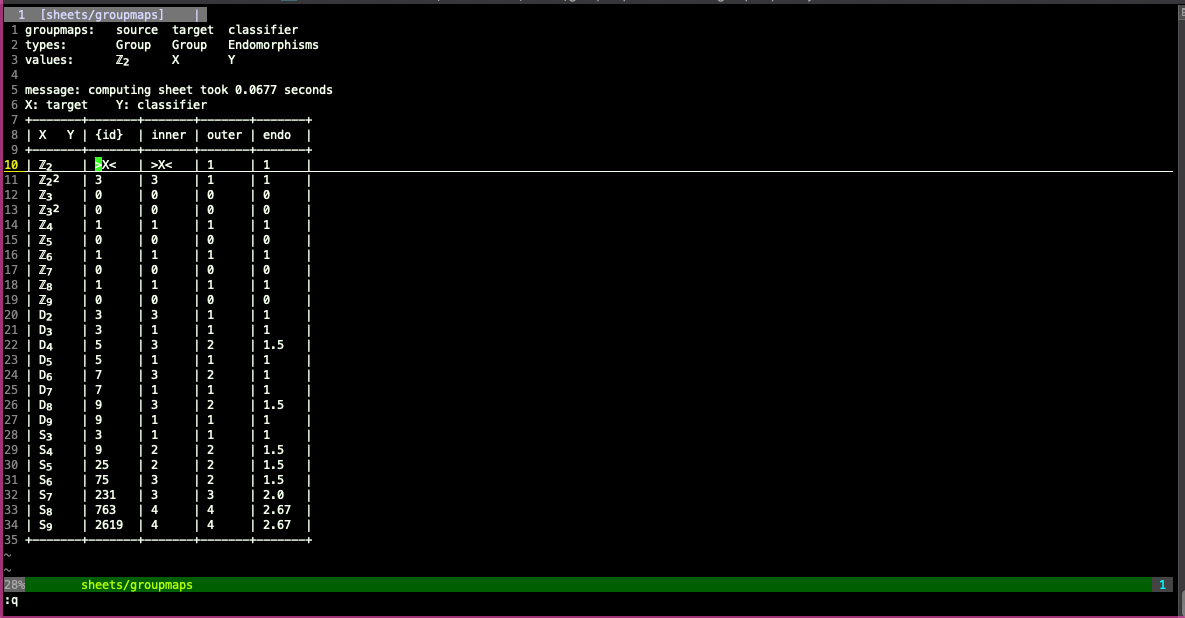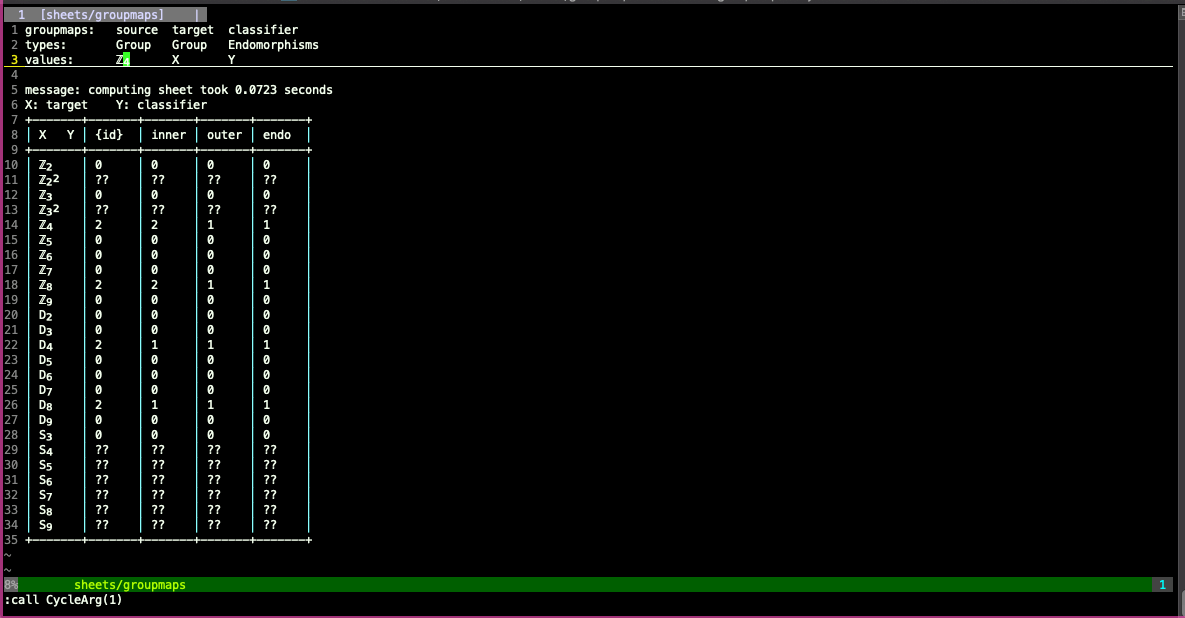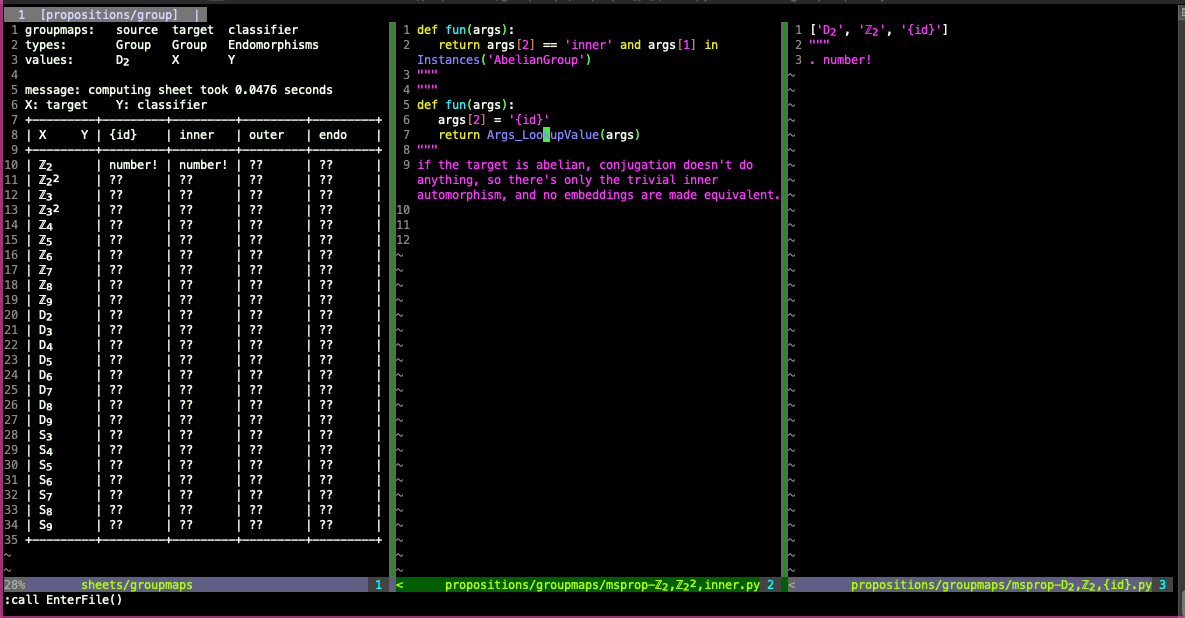
Example question: classifying maps up to homotopy

I had a math question with a few parameters.

Here's the question, though the details in this paragraph aren't necessary for the rest of this post: Given two topological spaces S and T, given two kinds B and C of functions (continuous, injective, surjective, homeomorphism), classify the functions from S to T of kind B up to paths through the function space C. For instance, if S = T = ℝ and B = C = injective, we're asking, what are the injective real functions f, up to equivalence by deformations of f that keep it injective during the whole deformation? (Answer: two, represented by λx.x and λx.-x (or ℤ₂, with composition as the operation).) (For this example, the topology on the function space is taken to be pointwise convergence, and only connected spaces are considered.)

There's very many questions of this form: one question for every selection of the parameters (two topological spaces and two properties of topological functions). This big space of questions is unwieldy because:

It's big---quadratic in the number of spaces and quadratic in the number of function types I want to think about.
For many values of the parameters S, T, B, and C, the question is trivial or uninteresting.
For many values, it's at least a little interesting.
It's not clear in advance which values make the question interesting.

Now, there are many cases that can be dealt with in one fell swoop, with a simple enough criterion, but not simply enough to eliminate possible values of parameters. (For example, classifying maps from the interval I to a 2-manifold is always trivial, but maps from I into a 1-manifold may not be trivial, and e.g. injections from the 1-manifold S₁ to a 2-manifold also aren't always trivial.)

I wanted to keep track of all these questions, and keep track of which ones I had or hadn't already answered. Especially, I wanted to keep track of somewhat general propositions I believed, such as "maps from contractible spaces are all equivalent (assuming the target is connected) via paths through arbitrary continuous functions", which is simple to apply but not so simple that I don't have to think for a moment. So I hacked together a minimal implementation of a multi-dimensional spreadsheet in vim, what I'm calling a "multisheet" (better name welcome).

General description of a multisheet

A multisheet is a generalization of spreadsheets from 2 dimensions to N dimensions. A spreadsheet is a function F from two variables, X and Y, to some value F(x,y). A spreadsheet is displayed as a 2-d table with the X and Y values on the x- and y-axis, with the value F(x,y) shown in cell (x,y). A multisheet is a function F from N variables to a value F(x₁, x₂, ..., x𝘯). A slice of a multisheet is displayed by specifying the values of N-2 of the arguments, and displaying the remaining two dimensions on the x- and y-axis, with the values of F shown in a cell (b,c) produced by setting the two unassigned arguments to b and c. (In other words, if F takes three arguments, we can display a slice by specifying the middle argument to be 7 and displaying the spreadsheet λx,y.F(x,7,y) .)

Using vim-multisheets

If you use vim / nvim, you can try vim-multisheets, an implementation of multisheets for vim. See https://github.com/tsvibt/vim-multisheets for instructions.

Please note the Warning section in the README; use at your own risk. (Improvements and implementations for other environments encouraged, if they're libre.)

The vim-multisheets implementation has multiple ways of specifying a value of the function F:

Leave the value unspecified, display as ??.
Specify the value at a single cell by associating a value with the list of parameters for that cell.
Specify the value on a (union of) rectangular prisms of cells, given as the cartesian product of possible values for each parameter.
Specify the value on a set of cells picked out by a python function that returns True or False.
As above, but instead of returning a fixed value on the set of cells, specify values on the set as a python function of the parameters.

In other words, vim-multisheets is a tool for partially specifying the values of a function and displaying slices of the graph of that function.

Using a multisheet to track beliefs

Using a multisheet made it more fun to think about the family of questions about maps between spaces. If I weren't tracking my answers, I'd keep bumping into questions that I'd already answered but that I didn't immediately realize I'd already answered. I'd have to repeatedly think of another combination of spaces and function types, think for a little while, and then remember "oh yeah, the source space is contractible" or something like that. Using a multisheet, it's easy to see whether I've already answered the question, and easy to answer a whole subset of questions in one go. That makes it easy to pretty immediately find a question I haven't already explicitly answered.

Example of specifying the value on a rectangular prism:

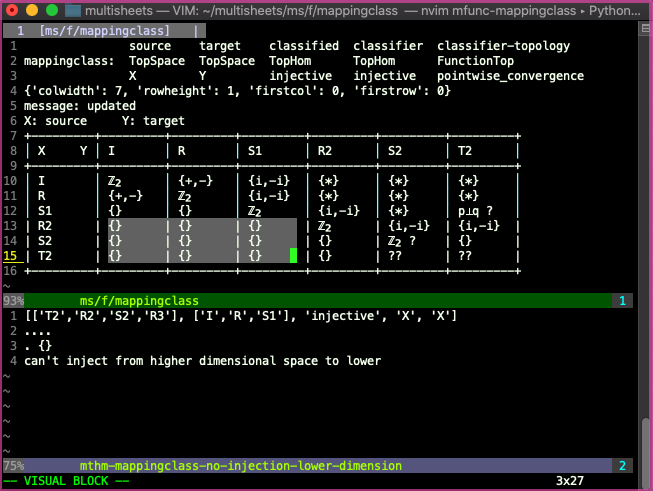
The first coordinate is specified to be in ['T2','R2','S2','R3'], the second in ['I','R','S1'], the third has to be injective, and the final two can be anything. The region controlled by this "proposition" is highlighted. The region extends in the final two dimensions, e.g. if we set the fourth argument to continuous:

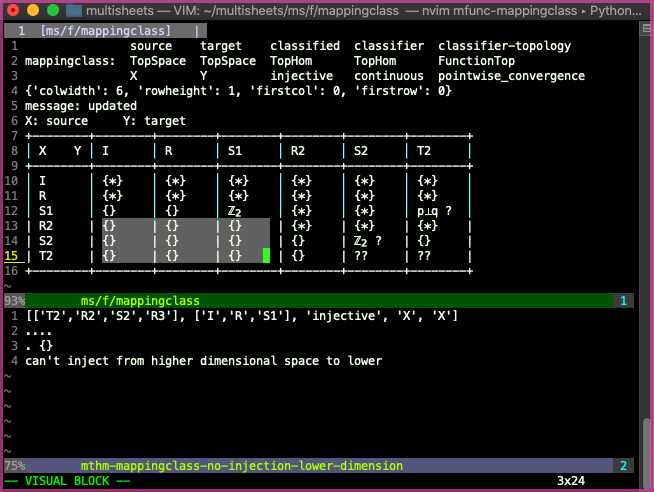
then we can see more of the region specified by this proposition.

Another example: classifying group embeddings

Another example of a question with multiple parameters (somewhat similar to the previous example): classifying group embeddings modulo post-composition with endomorphisms of the target. Let G and H be finite groups G and H, and let E ⊆ Endo(H) be a type of endomorphism of H ({identity}, inner automorphism, outer automorphism, or arbitrary endomorphism). How many embeddings f are there from G to H, modulo equivalence under post-composition by some m ∈ E? (This doesn't quite make sense for E = Endo(H), since it can happen that f⨟m = g is an embedding and yet there's no m' ∈ Endo(H) such that g⨟m' = f, but we can make up a way of "counting" the resulting posets.)

The teaser gif at the beginning of this post shows a multisheet for the group embeddings question.

As a (contrived) example of discovering contradictions in beliefs, say I had this (false) proposition specifying the number of embeddings D₃⟶ ℤ₅ up to inner automorphisms of ℤ₅:

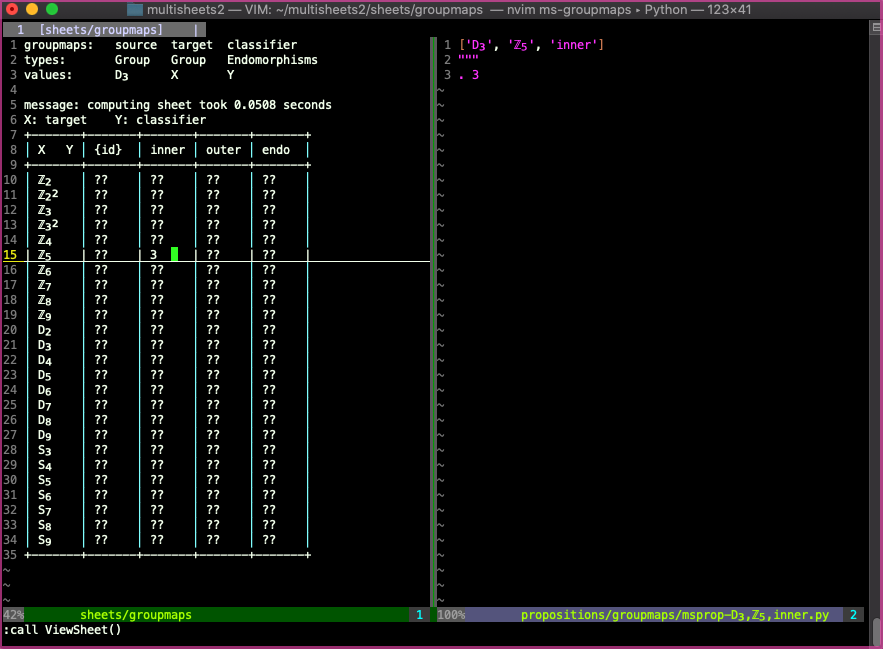
Then later I add another proposition saying that there are no embeddings D₃⟶ ℤ₅ (modding out by nothing, i.e. by the trivial group that's just the identity automorphism of ℤ₅):

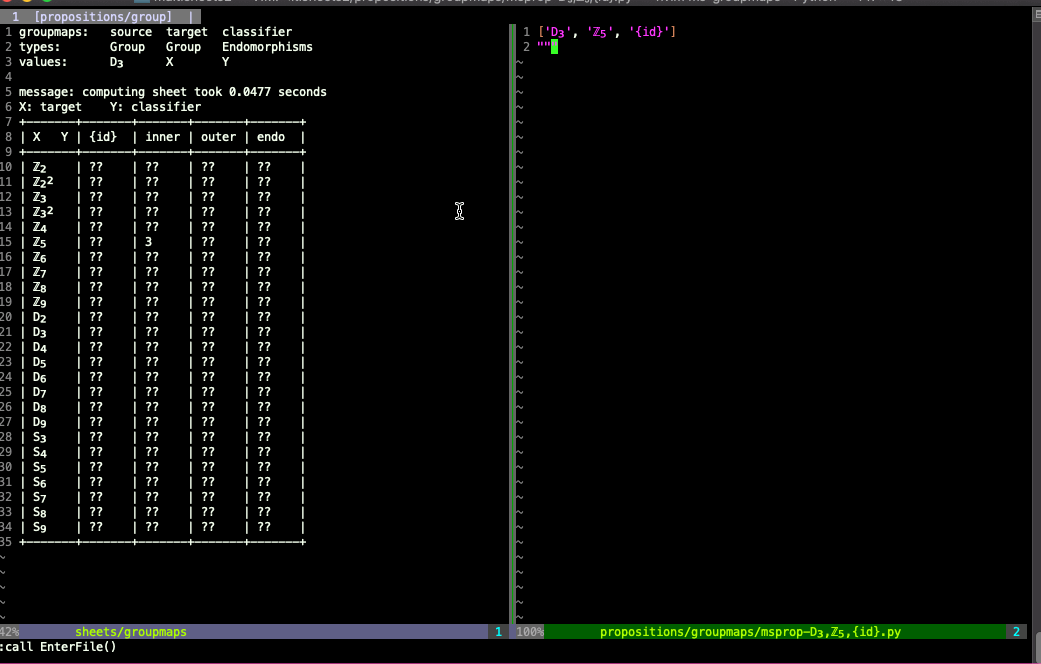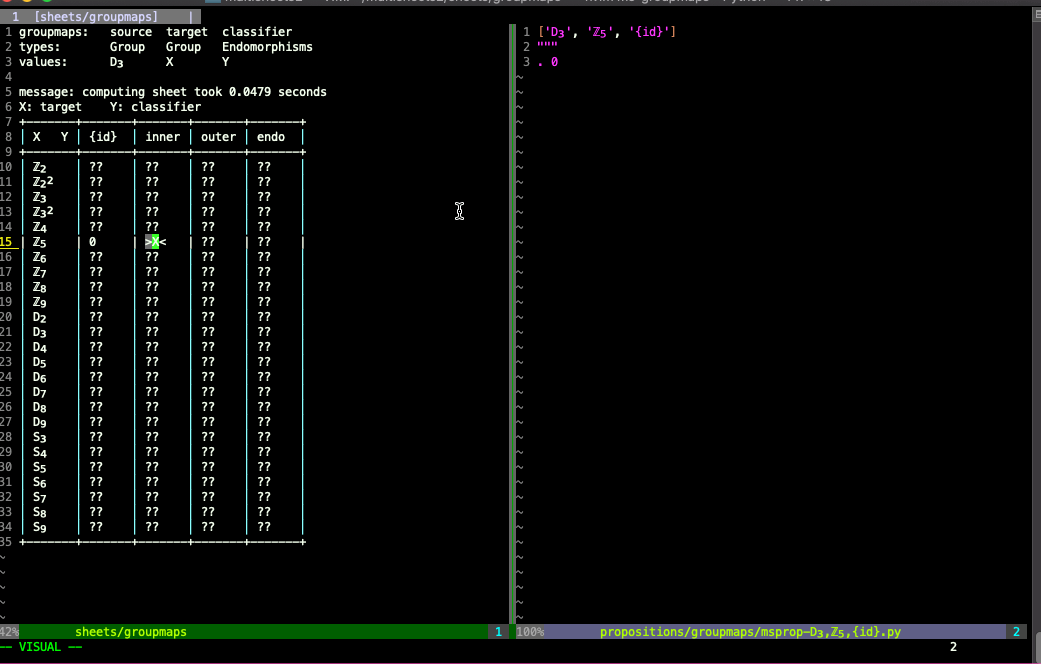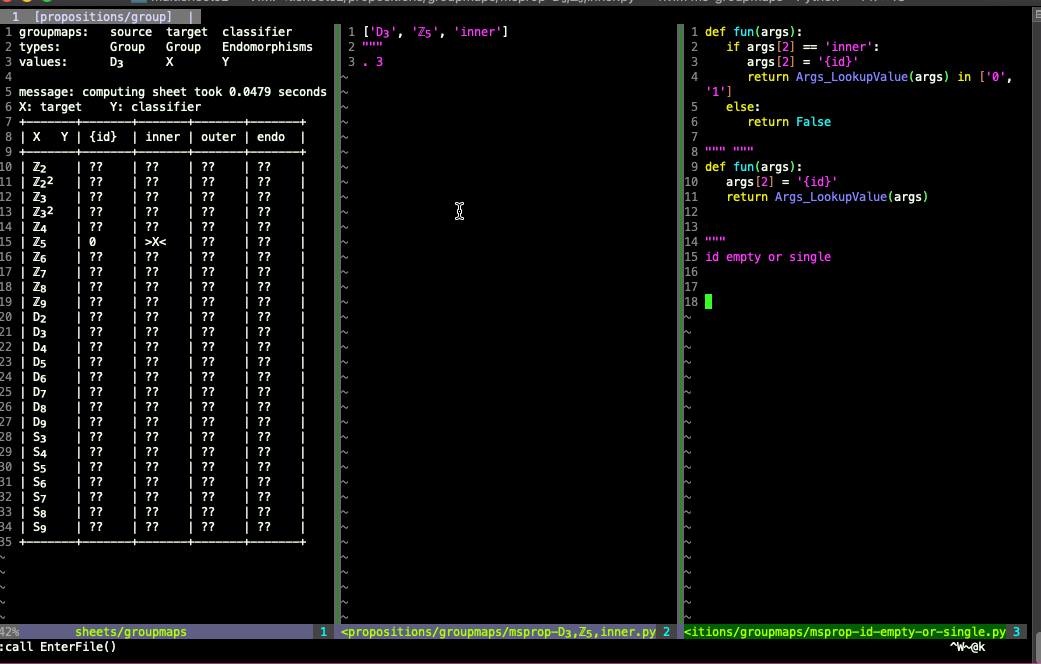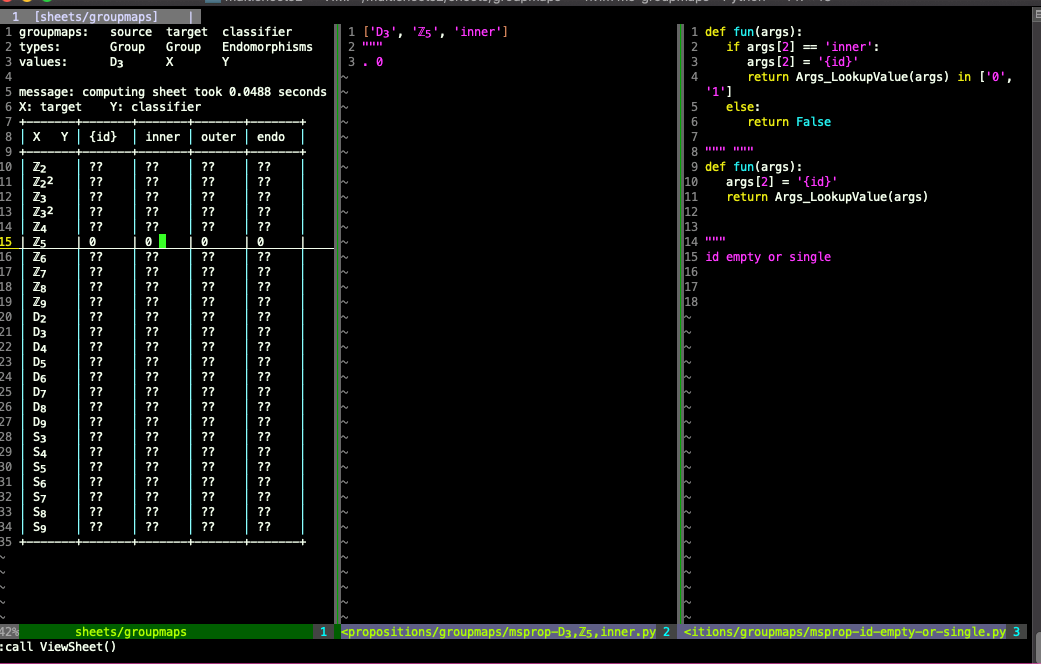
See the README of the github repo for more examples from this multisheet and instructions on how to use multisheets.

Context

Multisheets are an instance of the general idea of using software to help with thinking. More specifically, multisheets are an instance of using computers to mechanically compute consequences of formalized beliefs, and flag contradictions between beliefs. I might say more about this later, and might show another tool in the same theme, but for now I'll give a compressed description of a perspective on using computers to explore beliefs:

Computers are useful for mechanically computing consequences of beliefs if some interesting consequences of the beliefs can be formalized in an efficiently computable way. Automatically computing consequences of beliefs 1. points towards open questions, and 2. highlights contradictions between existing beliefs. This is different from the conception of automated theorem proving motivated by verification, because it assumes beliefs as stated to be largely correct, and operates on that assumption until contradictions are revealed.

In verification, we formalize statements and proofs in a context that's expressive enough that we can compactly and faithfully formalize concepts---that is, we encode concepts so that the theorems we'd want to show about those concepts are in fact logical consequences of the definitions we've given. Since the language is expressive, there are very many consequences, and the proofs of implications may be complex. Since proofs may be complex, if we're trying to get the benefits of demonstrating implications without making any further fundamental assumptions (e.g., confidence that our theorems actually follow from our explicit understanding (our formalization) of the objects in question), then we have a lot of work to do, namely we have to spell out a bunch of complex proofs, hopefully with help from the computer.

In the alternative perspective of using computers for belief propagation rather than belief verification, we do something sort of like putting assert or sorry everywhere. Then we have the computer look at a set of questions (propositions, say) and find which of them are and are not answered as consequences of our asserted beliefs, and show us answers and open questions; and we have the computer locate and show us minimal sets of contradictory asserted beliefs. This is potentially more fun, in that it points to questions you haven't answered, and points to obvious major logical contradictions present in your high-level beliefs. (And sometimes it does those things efficiently compared to more expressive verification, by focusing on a simpler language, at the expense of making some consequences impossible to automatically find or verify.) I hope that in general there will be more tools that support our thinking at all the different levels that are relevant to what we're interested in.

Search This Blog

Multisheets: multi-dimensional spreadsheets for belief tracking